얼마나 멀리서 유성을 볼 수 있습니까?
>나는 이메일을 받는다.
세라피나와 검은 망토 읽기 레벨
대부분은 다양한 유형의 질문을 하고 있으며 그 중 대부분은 대답하기 매우 간단합니다(사실 많은 경우 인터넷 검색, 힌트 힌트로 답을 얻을 수 있음). 그러나 때때로 나는 대답하기 더 어려운 질문을 받거나 심지어 나 자신에 대해 궁금했지만 결코 알아내지 못한 질문을 받습니다.
그래서 나는 Bad Reader Dean Lewis로부터 유성에 대한 질문을 받았을 때 꽤 흥미를 느꼈습니다. 2018년 페르세우스 왕조 유성우 동안 그는 약 1,000km 떨어진 가족과 떨어져 있었습니다. 그가 유성을 본다면 더 먼 곳에서 같은 것을 볼 수 있습니까?
짧은 대답은 다음과 같습니다. 예! 긴 대답은 ... 수학입니다. 멋지고 재미있는 수학.
그리고 이 기사가 게시될 때 2018년 연례 쌍둥이자리 유성우가 오늘 밤 최고조에 달하는 것을 보았을 때 이것을 파악하는 것이 적절하다고 생각합니다.
단기 집중 천문학: 유성, 운석, 운석, 오 마이!
지구가 완벽하게 평평하다면 원칙적으로 지구 가장자리까지 유성을 볼 수 있습니다. 당신이 지상에 있는 한, 아주 조금이라도 당신의 시야는 당신 옆에 있는 행성의 모든 평방 센티미터에 도달하므로 모든 유성은 모든 사람이 볼 수 있습니다. 실제로 공기는 완벽하게 투명하지 않기 때문에 멀리서 보면 먼지가 너무 많이 껴서 아무것도 보이지 않습니다.
그러나 지구는 평평하지 않습니다. 진지하게! 그것은 둥글다. 그리고 대기는 그것을 조개껍데기처럼 둘러싸고 높이가 올라갈수록 점점 가늘어지며 결국 쇠퇴합니다. 그 높이는 공간의 정의에 따라 다릅니다. 그러나 우리는 과학을 알고 있기 때문에 약간의 속임수를 쓸 수 있습니다. 소나기와 같은 유성은 지상에서 약 100km를 태우는 경향이 있습니다. 그 높이는 얼마나 큰지를 포함하여 많은 것에 달려 있습니다. 유성체 (우주를 통과하는 행성간 파편의 단단한 조각), 얼마나 빨리 움직이는지, 어떤 각도로 대기에 진입하는지 등입니다. 하지만 100km라고 합시다.
유성이 당신에게 가장 가까울 수 있는 것은 당신이 그 바로 아래에 있고 그 다음 100km(당신의 천정에서) 직선으로 있는 경우입니다. 그것이 천정에서 더 멀리 타 오르면 그것은 당신에게서 더 멀리 떨어져 있어야합니다. 가장 멀리서 유성을 볼 수 있는 것은 당연합니다. 따라서 정확히 지평선 위에 있는 경우입니다.
그 형상은 다음과 같습니다(참고: 크기 조정이 아님).
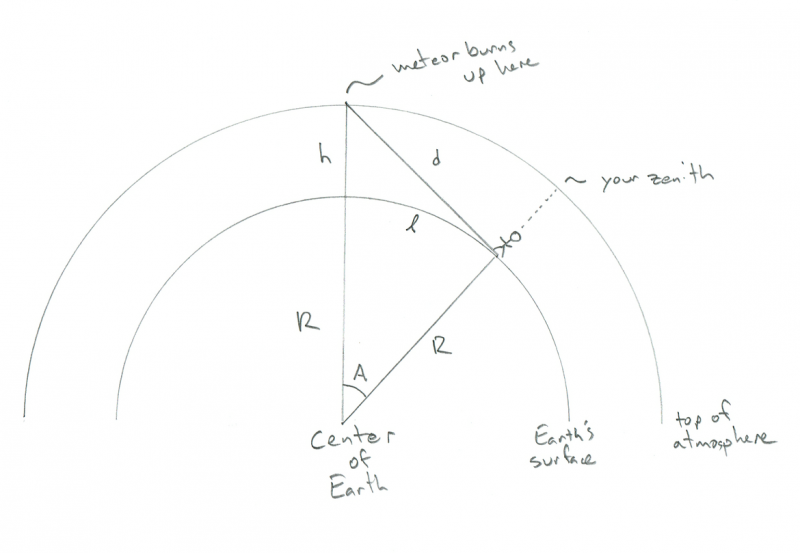
불타는 유성을 관찰하는 관찰자의 기하학을 보여주는 개략도. 크레딧: Phil Plait
구부러진 지구의 표면에 인간이 서 있는 작은 막대기 모양을 볼 수 있습니다. 그 위에 (또한 구부러진) 대기가 있습니다. 이 다이어그램에서 R은 지구의 반지름(6,4000km), h는 유성이 타는 높이(100km), d는 당신에서 유성까지의 거리입니다. A는 지구에서의 당신의 위치와 그 위의 유성의 위치 사이의 각도이고, 초서체 l(길이와 같음)은 유성이 바로 머리 위에 있게 하기 위해 걸어야 하는 거리입니다(나는 그것이 이상한 것처럼 보인다는 것을 압니다. 알고 싶지만 참아주세요). 이상하게도 여기에서 d를 몰라도 필요한 모든 것을 계산할 수 있지만 자, 유성이 얼마나 멀리 있는지 아는 것이 멋지지 않습니까?
이 모든 것의 핵심은 유성과 당신과 지구의 중심 사이의 각도가 직각이라는 것을 보는 것입니다. 그것은 유성이 당신이 보는 수평선 위에 있기 때문입니다(또는 재미있는 전문 용어를 선호하는 경우 R이 교차하는 내부 원의 접선에 있음). 그것은 삼각형을 직각삼각형으로 만들고, 고등학교 수학을 기억한다면 모든 변과 각을 찾을 수 있다는 것을 의미합니다!
기억하다 피타고라스 정리 ? 직각 삼각형에서 빗변의 길이의 제곱은 다른 두 변의 제곱의 합과 같습니다.*. 삼각형에서 빗변은 R+h이고 다른 변은 R과 d입니다.
그래서
(R+h)2= 디2+ R2
또는 왼쪽을 곱합니다(사용 박 ):
NS2+ 2Rh + h2 = d2+ R2
유성이 당신에게서 얼마나 멀리 떨어져 있는지 확인하기 위해 d를 풉니다. R2는 양쪽에 있으므로 취소하여 얻으십시오.
NS2= 2Rh + h2
또는
d = 제곱근(2Rh + h2)
글쎄, 우리는 그 모든 숫자를 알고 있습니다! 플러그 앤 처그, 베이비:
d = 제곱근(2 x 6,400 x 100 + 10,000) = 1,136km
아하! 이것은 수평선에서 유성을 본다면 1,100km 이상 떨어져 있음을 의미합니다! 그것은 먼 길이며 기술적으로 가장 멀리 떨어진 곳에서 지상에서 유성을 볼 수 있습니다.
이제 필기체 l을 찾아봅시다. 먼저 각도 A를 알아야 합니다. 이를 위해서는 약간의 삼각법이 필요합니다. 많은 삼각 아이덴티티 이것을 알아내는 데 사용할 수 있지만 내가 가장 좋아하는†직각 삼각형에서 각도의 사인은 반대쪽의 길이를 빗변의 길이로 나눈 값입니다. 따라서 해당 비율을 얻으면 역 사인(또는 아크사인)을 취하여 각도를 얻을 수 있습니다.
죄 (A) = d / (R + h)
그래서
A = 없음-1(d / R + h)
다시 Plug-n-chug하면 A = 10°가 됩니다. 그것은 지구 표면의 적절한 덩어리입니다!
이제 우리는 필기체 l을 얻을 수 있습니다. 지구 둘레는 360°이고 지구의 둘레는 2 x pi x 반지름 = 40,192km이므로 다음이 있습니다.
40,192km / 360° = 1도당 112km
이는 차례로 10° = 1,120km를 의미합니다. 이는 d에 매우 가깝습니다. 이는 그다지 놀라운 일이 아닙니다. 그림은 과장되어 있지만 실제로 우리를 덮고 있는 공기의 껍질은 지구의 크기에 비해 작습니다. 도면을 축척에 맞게 만들면 d와 l의 길이가 실제로 매우 가깝다는 것을 알 수 있습니다.
좋아, 그럼 내가 왜 l을 찾는 데 열중하고 귀찮게 하는 거지? 원래 질문 때문에! 그 모든 수학을 잊었다면 두 사람이 얼마나 멀리 떨어져 있으면서도 같은 유성을 볼 수 있습니까?
그렇다면 유성은 그들 사이에, 그리고 각각의 지평선에 직접 있을 것입니다. 해당 지오메트리는 다음과 같습니다.
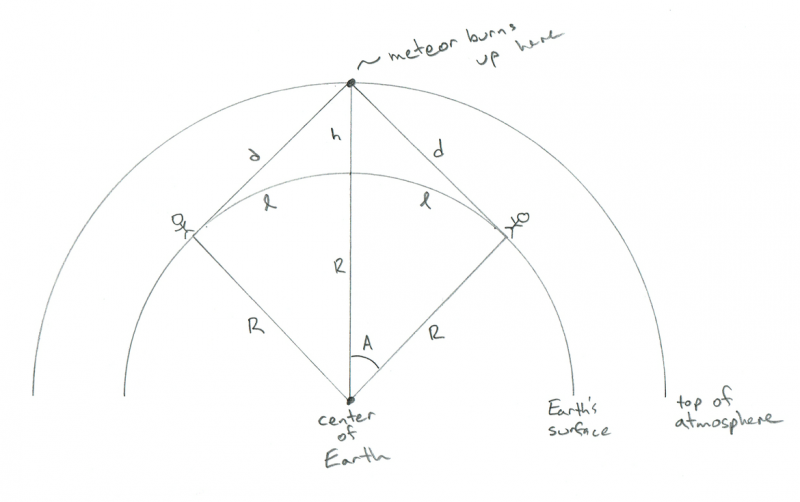
두 관찰자 사이에서 정확히 불타는 유성을 관찰하는 두 관찰자의 기하학을 보여주는 개략도. 크레딧: Phil Plait
아하! 이제 내가 왜 L을 원하는지 알 것입니다! 두 사람의 거리는 2xl! 이제 우리는 답을 얻었습니다.
두 사람이 같은 유성을 보기 위해서는 2 x 1,120 = 2,240km 이상 떨어져 있을 수 없습니다. 예를 들어 워싱턴 DC와 덴버 사이의 거리와 매우 가깝습니다. 와.
덧붙여서, 원근법(문자 그대로)의 변경은 유성의 관점에서 2,240km 너비의 지구를 볼 수 있음을 의미합니다(지구의 동쪽 가장자리에 DC, 서쪽 가장자리에 덴버). 꽤 괜찮은데.
그리고 그것은 우리를 Dean의 질문에 대한 실제 답으로 이끕니다. 만약 그가 그의 가족으로부터 1,000km 떨어져 있다면, 그렇습니다. 기술적으로 그들은 같은 유성을 볼 수 있습니다. 어떻게에 대한?
이제 이것은 다시 공기가 완벽하게 깨끗하고 실제로는 불가능한 모든 것을 가정합니다. 따라서 이 수학은 이상적인 상황을 나타냅니다(유성이 정확히 그 사이에 있다는 생각 포함).
좀 더 현실적으로 가자. 유성이 두 관찰자 모두에게 수평선 위 45°의 고도에서 하늘에서 타오른다고 가정해 봅시다. 서로 얼마나 멀리 떨어져 있을까요? 음, 유성이 정확히 그들 사이에 있다고 다시 가정하면 기하학은 다음과 같습니다.
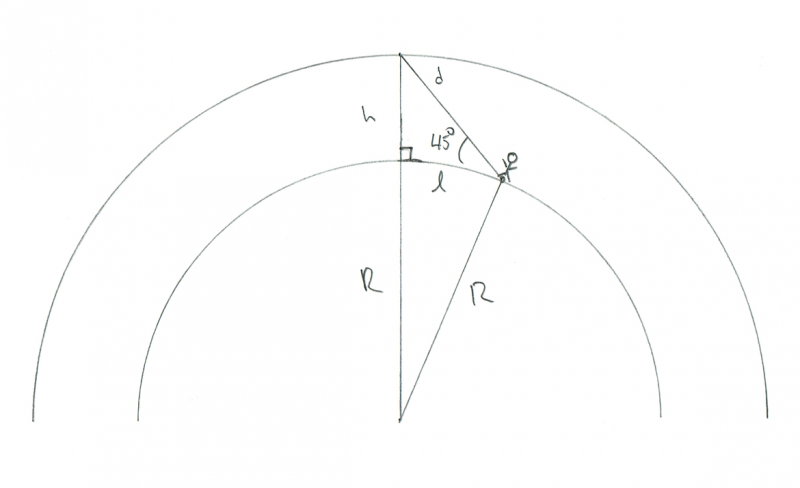
수평선 위 45°에서 불타는 유성을 관찰하는 관찰자의 기하학을 보여주는 개략도. 크레딧: Phil Plait
이것은 실제로 해결하기가 더 어렵지만 다른 트릭을 알고 있습니다. l이 작다고 가정하면 지구의 곡률이 중요하지 않을 것입니다. 예를 들어, 마당에 있는 두 나무 사이의 거리를 알고 싶다면 지구가 구부러져도 상관없습니다. 그렇게 작은 거리에서는 평평하다고 가정할 수 있습니다. 여기서 그 가정을 해보자.
그 경우에, 우리는 또 다른 직각 삼각형을 가지고 있지만, 이번에는 직각이 유성 아래의 것입니다. 나는 심지어 작은 사각형 표기법으로 다이어그램에 레이블을 붙였습니다. 따라서 그것이 90° 각도이고 유성에 대한 우리의 각도가 45°이면 마지막 각도(유성에서 관찰자까지)도 45°입니다. 이것은 이것이 이등변 삼각형이어야 함을 의미하므로 l과 h는 동일합니다! h가 100km라는 것을 알고 있으므로 l도 마찬가지입니다.
그리고 그것은 우리의 두 관찰자 사이의 거리가 그 두 배인 200km라는 것을 의미합니다.
덧붙여서, 이 경우 유성까지의 거리는 약 141km입니다. 나는 그것을 독자에게 연습으로 남겨 두겠습니다.
원칙적으로 이것은 유성이 수평선에서 얼마나 높은지와 그것이 타버린 고도를 알면 거리를 계산할 수 있음을 의미합니다(또는 거리를 알면 높이를 알 수 있음). 그 삼각법은 꽤 복잡합니다. 오늘 수학을 충분히 했다고 생각합니다.
그러나 약간의 고등학교 수학이 그렇게 재미있는 응용 프로그램이 될 수 있다고 생각하는 것은 멋진 일입니다. 그리고 나는 이별이 너무 멀지 않은 한, 별똥별을 보는 것을 다른 사람과 공유 할 수 있다는 것을 아는 것이 시적이고 낭만적이라는 것을 인정합니다. 정말 멋진 생각입니다.
* 입력 오즈의 마법사 , 허수아비가 틀렸어 ~ 후에 그는 뇌를 얻었다.
† 의 강의 나는 좋아하는 trig 아이덴티티가 있습니다. 무엇 당신이야?













